(5.2)

chapter (5.2) will be added about few hours later

Combination Circuit Design, Design Procedure, Code Converter Example (5.1)

Combination Circuit Design

• Design of a combinational circuit is the development of a circuit from a description

of its function.

– “design an excess-123 encoder”

– “provide a circuit that will multiplex one of three 8-bit input buses onto an 8-bit output bus.”

Design Procedure

1. Determine the required number of inputs and outputs and assign variables to them.

2. Derive the truth table that defines the required relationship between inputs and outputs.

3. Obtain and simplify the Boolean function.

4. Draw the logic diagram.

5. Verify the correctness of the design.

Code Converter Example

• Design a circuit that converts a binary-coded decimal  (BCD) codeword to its corresponding excess-3 codeword.
• If the input is a number n expressed in BCD, the output should be the number n+3 expressed in binary.
• We need 4 input variables (a,b,c,d) and 4 output functions w(a,b,c,d),x(a,b,c,d),y(a,b,c,d),z(a,b,c,d)).

By convention, a and w are the most significant bits of the input and output, respectively.

• The truth table relating the input and output variables is shown at right.
• Note that the outputs for inputs 1010 through 1111 are don't cares.

The K-maps for w( ), x( ), y( ), and z( ) can be constructed with don't cares.The simplified Boolean functions derived from the K-maps are:

– z = d’

– y = cd + c’d’

– x = b’c + b’d + bc’d’

– w = a+bc+bd

Combinational Circuits (5)

• A combinational circuit consists of logic gates whose outputs at any time are determined by the inputs using logic operations.
• For n input variables, there are 2ⁿ possible binary input combinations.
• For each binary combination of the input variables, there is one possible binary value

on each output.

•  Hence, a combinational circuit can be described by

1. a truth table that lists the output values for each combination of the input variables, or

2. m Boolean functions, one for each output  variable.

Combinational Circuit Analysis

• Analysis of a combinational circuit is the determination of the Boolean function that

the circuit implements.

• The analysis starts with a given logic circuit diagram and ends with a set of Boolean

functions or (equivalently) a truth table.

 Example:

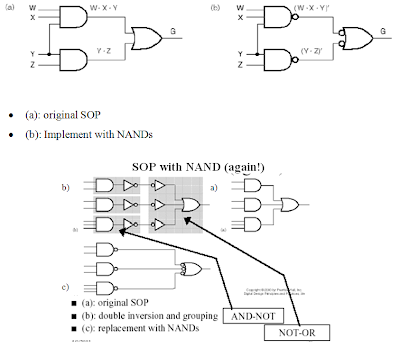
Multilevel NAND Circuits (4.3)

1. Convert all AND gates to NAND gates with AND-NOT graphic symbols.

2. Convert all OR gates to NAND gates with NOT-OR graphic symbols.

3. Check all the bubbles in the diagram.  For every bubble that is not counteracted by

another bubble along the same line, insert a NOT gate or complement the input literal

from its original appearance.

Example

• Use NAND gates and NOT gates to implement Z = E’F(AB+C’+D’)+GH

Problem. Implement the circuit with the truth table

Two-Level NAND Gate Implementation Example (4.2)

• _f(X,Y,Z) = Sm(0,6)

1. Express f in SOP form: f = X’Y’Z’ +XYZ’

2. Obtain the AND-OR implementation for f.

3. Add bubbles and inverters to transform AND-OR to NAND-NAND gates.

• Two-level implementation with NANDs

Two-Level NOR Gate

Implementation Example

• f(X,Y,Z) = ПM(0,6)   
• 1. Express f’ in SOP form:

1. f’ = Sm(1,2,3,4,5,7)= X’Y’Z + X’YZ’ + X’YZ + XY’Z’ + XY’Z + XYZ

2. f’ = XY’ + X’Y + Z

2. Take the complement of f’ to get f in the POS form: f = (f’)' = (X'+Y)(X+Y')Z'

3. Obtain the OR-AND implementation for f.

4. Add bubbles and inverters to transform OR-AND implementation to NOR-NOR implementation.

• Two-level implementation with NORs

AND-OR (SOP) Emulation with NANDs (4.1)

Gates (4)

Product of Sums Simplification (3.5)

·         Use sum-of-products simplification on the zeros of the function in the K-map to get f’.

·         Recall that the complement of a boolean function can be obtained by (1) taking the

dual and (2) complementing each literal. (aka generalized DeMorgan’s rule).

·         Complement f’ using DeMorgan’s Theorem to get f.

Example

·         Find a simplified product-of-sums expression for f(a,b,c,d) = M(0,1,7,15).

·         (f(a,b,c,d))’ =a’b’c’ + bcd

·         f_dual (a,b,c,d) = (a’+b’+c’)(b+c+d)

·         f(a,b,c,d) = (a+b+c)(b’+c’+d’)

Minimization with don’t cares (3.4)

•  Treat don't cares as if they are 1s to generate PIs.
• Delete PI's that cover only don't care minterms.
• Treat the covering of remaining don't care minterms as optional in the selection process (i.e. they may be, but need not be, covered).

Use of Don't Care Conditions (3.3)

There may be a combination of input values which:

·         will never occur

·         if they do occur, the output is of no concern.

·         The function value for such combinations is  called a don't care.

·         They are denoted with a d (or x, or –). Each d may be arbitrarily assigned the value 0 or

1 in an implementation.

Systematic Procedure for Simplifying Boolean Functions (3.2)

1. Generate all PIs of the function.

2. Include all essential PIs.

3. For remaining minterms not included in the essential PIs, select a set of other PIs (which have already been generated earlier) to cover them, with minimal overlap in the set.

4. The resulting simplified function is the logical OR of the product terms selected above.

Example

·         f(a,b,c,d) = m(0,1,2,3,4,5,7,14,15).

·          Five grouped terms, not all needed.

·         3 shaded cells covered by only one term

·         3 EPIs, since each shaded cell is covered by a different term.

·         F(a,b,c,d) = a’c’ + a’d + a’b’ + abc  (EPIs are indicated in bold)

PI  a’d must be added to EPIs (because it covers remaining 1 and is larger than other PI (bcd), which covers the same 1)

Essential Prime Implicant (3.1)

·         An essential prime implicant of a function is a prime implicant that contains at least one minterm not contained in any  other prime implicant.

·         To find essential prime implicants, we first generate all prime implicants of a function, and then select those prime implicants that contain at least one 1 that is not covered by any other prime implicant.

·         For the previous example, the PIs are d’, bc, and ab’c’; all of these are essential.

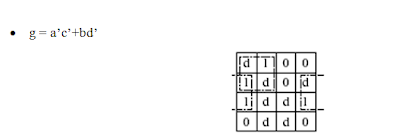
Example

·         Consider f2(a,b,c,d), whose K-map is shown at right.

·         The only essential PI is bd’.

Implicants and Prime Implicants (3)

·         An Implicant of a function is a product term of the function.

·         A product term is called an implicant, because whenever it takes the value 1, the function also takes the value 1, hence the term implies the function’s value.

·         A Prime Implicant of a function is an implicant of the function not contained (entirely!) in any “larger” implicant.

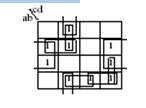
Example

·         Consider function f(a,b,c,d) whose K-map is shown below.  

·         c’d’ is not a prime implicant because c’d’ is contained in d’.

·         bcd is not a prime implicant because bcd is contained in bc.

·         d’, bc, and ab’c’ are prime implicants.