Exercise 1. (1.13)

• Prove with the aid of the laws of boolean algebra that f1(a,b,c)=f2(a,b,c), where f1(a,b,c)=a’bc+ab’c+ab’c’+a’bc’++abc’+abc and f2(a,bc)=a+b ;
• The following 2 problems refer to the table :

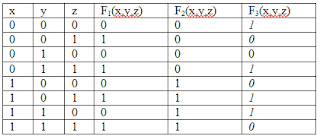
 (1)  Write F₁(x,y,z) as a sum of minterms.

 (2)  Write F₂(x,y,z) as a product of maxterms.       

(3) Convert the sum-of-products (SOP) from standard to canonical form:

      f1(a,b,c)=ab+c ;

      f2(a,b,c)=a+b’c+a’bc ;

(4) Convert the product-of sums (POS) from standard to canonical form:

      f3(a,b,c)=a(b+c’);