Essential Prime Implicant (3.1)

·         An essential prime implicant of a function is a prime implicant that contains at least one minterm not contained in any  other prime implicant.

·         To find essential prime implicants, we first generate all prime implicants of a function, and then select those prime implicants that contain at least one 1 that is not covered by any other prime implicant.

·         For the previous example, the PIs are d’, bc, and ab’c’; all of these are essential.

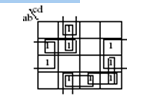
Example

·         Consider f2(a,b,c,d), whose K-map is shown at right.

·         The only essential PI is bd’.